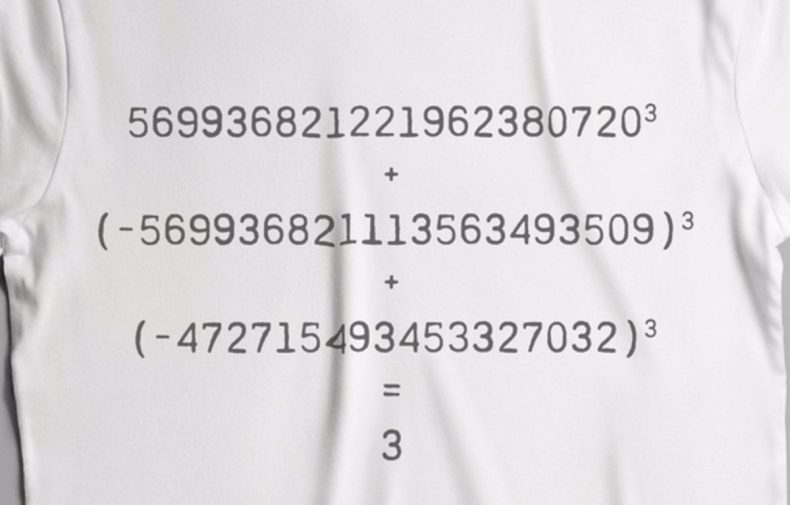Tras resolver la última pieza del acertijo matemático de la ecuación conocida como ‘suma de cubos’ para 42 en 2019, los mismos investigadores han superado el reto con una nueva solución para 3.
La solución de 21 dígitos al problema de hace décadas sugiere que existen muchas más soluciones.
En matemáticas existe una ecuación polinomial cuya respuesta, 42, había eludido de manera similar a los matemáticos durante décadas. La ecuación x3 + y3 + z3 = k se conoce como el problema de la suma de cubos. Aunque aparentemente sencilla, la ecuación se vuelve exponencialmente difícil de resolver cuando se enmarca como una «ecuación diofántica», un problema que estipula que, para cualquier valor de k, los valores de x, y y z deben ser números enteros.
Cuando la ecuación de suma de cubos se enmarca de esta manera, para ciertos valores de k, las soluciones enteras para x, y y z pueden crecer hasta números enormes. El espacio numérico en el que los matemáticos deben buscar estos números es aún mayor y requiere cálculos complejos y masivos.
A lo largo de los años, los matemáticos se las habían arreglado a través de varios medios para resolver la ecuación, ya sea encontrando una solución o determinando que no debía existir una solución, para cada valor de k entre 1 y 100, excepto 42.
En septiembre de 2019, Andy Booker (Universidad de Bristol) y Drew Sutherland (MIT), aprovechando la potencia combinada de medio millón de computadoras domésticas en todo el mundo, encontraron por primera vez una solución a 42. El avance ampliamente reportado estimuló al equipo a abordar una solución aún más difícil, y de alguna manera más problema universal: encontrar la siguiente solución para 3.
Booker y Sutherland han publicado las soluciones para 42 y 3, junto con varios otros números superiores a 100, esta semana en Proceedings of the National Academy of Sciences.
UN RETO ESTABLECIDO EN 1953
Las dos primeras soluciones para la ecuación x3 + y3 + z3 = 3 pueden ser obvias para cualquier estudiante de álgebra de secundaria, donde x, y y z pueden ser 1, 1 y 1, o 4, 4 y -5. Sin embargo, encontrar una tercera solución ha dejado perplejos a los teóricos de los números expertos durante décadas, y en 1953 el acertijo llevó al matemático pionero Louis Mordell a hacer la pregunta: ¿Es posible saber si existen otras soluciones para 3?
«Esto fue algo así como Mordell arrojando el guante», dice Sutherland en un comunicado. «El interés en resolver esta cuestión no es tanto por la solución en particular, sino por comprender mejor qué tan difíciles son estas ecuaciones para resolver. Es un punto de referencia con el que podemos medirnos».
A medida que pasaban las décadas sin nuevas soluciones para 3, muchos empezaron a creer que no había ninguna. Pero poco después de encontrar la respuesta a 42, el método de Booker y Sutherland, en un tiempo sorprendentemente corto, dio como resultado la siguiente solución para 3:
5699368212219623807203 + (-569936821113563493509) 3 + (-472715493453327032) 3 = 3
El descubrimiento fue una respuesta directa a la pregunta de Mordell: Sí, es posible encontrar la siguiente solución a 3 y, lo que es más, aquí está esa solución. Y quizás de manera más universal, la solución, que involucra números gigantes de 21 dígitos que no era posible tamizar hasta ahora, sugiere que existen más soluciones para 3 y otros valores de k.
«Hubo serias dudas en las comunidades matemáticas y computacionales, porque [la pregunta de Mordell] es muy difícil de probar», dice Sutherland. «Los números se vuelven tan grandes tan rápido. Nunca encontrarás más que las primeras soluciones. Pero lo que puedo decir es que, habiendo encontrado esta única solución, estoy convencido de que hay infinitamente muchas más».
Para encontrar las soluciones para 42 y 3, el equipo comenzó con un algoritmo existente, o un giro de la ecuación de suma de cubos en una forma que creían que sería más manejable de resolver:
k – z3 = x3 + y3 = (x + y) (x2 – xy + y2)
Este enfoque fue propuesto por primera vez por el matemático Roger Heath-Brown, quien conjeturó que debería haber infinitas soluciones para cada k adecuado. El equipo modificó aún más el algoritmo al representar x + y como un único parámetro, d. Luego redujeron la ecuación dividiendo ambos lados por dy manteniendo solo el resto _una operación en matemáticas denominada «módulo d» – dejando una representación simplificada del problema.
«Ahora puede pensar en k como una raíz cúbica de z, módulo d», explica Sutherland. «Así que imagina trabajar en un sistema aritmético en el que solo te importa el resto módulo d, y estamos tratando de calcular una raíz cúbica de k».
Con esta versión más elegante de la ecuación, los investigadores solo necesitarían buscar valores de dyz que garantizarían encontrar las soluciones finales ax, y y z, para k = 3. Pero aún así, el espacio de números en el que tendrían que buscar sería infinitamente grande.
Así, los investigadores optimizaron el algoritmo mediante el uso de técnicas matemáticas de «tamizado» para reducir drásticamente el espacio de posibles soluciones para d.
«Se trata de una teoría de números bastante avanzada, que utiliza la estructura de lo que sabemos sobre los campos numéricos para evitar buscar en lugares donde no necesitamos mirar», dice Sutherland.
El equipo también desarrolló formas de dividir de manera eficiente la búsqueda del algoritmo en cientos de miles de flujos de procesamiento en paralelo. Si el algoritmo se ejecutara en una sola computadora, habría llevado cientos de años encontrar una solución para k = 3. Al dividir el trabajo en millones de tareas más pequeñas, cada una de las cuales se ejecuta de forma independiente en una computadora separada, el equipo podría acelerar aún más su búsqueda.